Two Adjacent Angles That Form A Straight Line
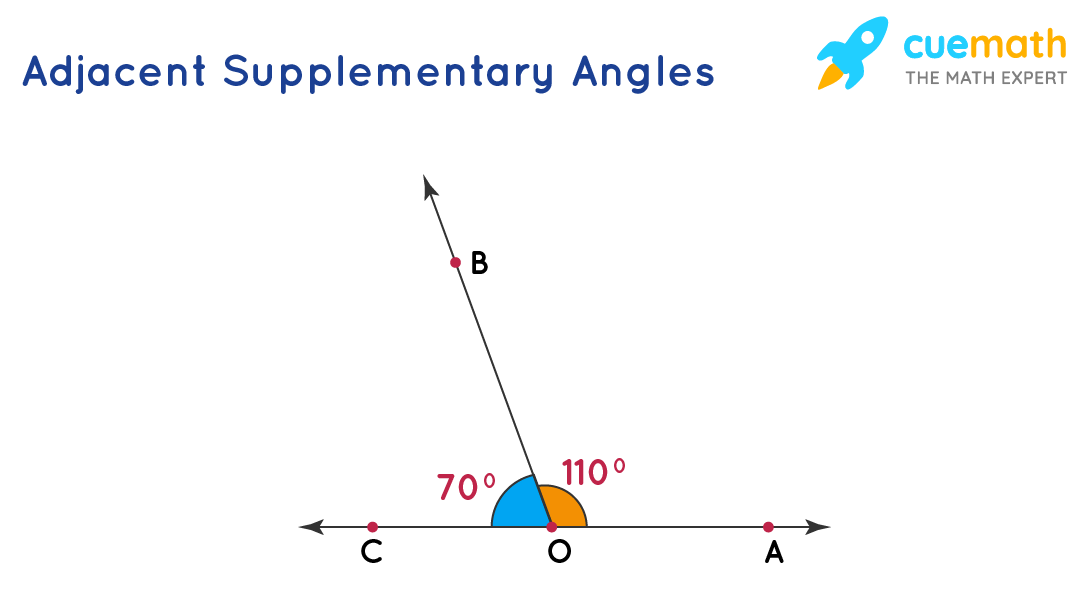
Two Adjacent Angles That Form A Straight Line - Web two adjacent angles that form a straight line? Therefore, a straight line (straight angle) has a measurement of 180 de nition: Web given that two adjacent angles whose sides form a straight line, then their sum is 1804. Adjacent angles always refer to a pair of angles. 3x + 3 (36) = 108 degrees. Web in geometry, a linear pair of angles is a pair of adjacent angles formed when two lines intersect each other. If the exterior sides of two acute adjacent angles form perpendicular rays, then these angles are complementary. Those two angles are now side to side, and they form a straight line from one endpoint to another endpoint. Web angles on one side of a straight line always add to 180 degrees. Web math, microeconomics or criminal justice.
The equation now is very simple. Adjacent angles are formed when two angles have a common. They are called supplementary angles. If the exterior sides of two. Web any two angles are said to be supplementary angles when their sums add up to 180° the “s’ in supplementary angles stand for straight line, this means that they. Web solution given, the ratio of two adjacent angles on a straight line = 5 : 2x = 2 (36) = 72 degrees. A straight line has 180 degrees each side and two adjacent angles forming 180. Which of the following is the property or definition that justifies the statement? If the exterior sides of two acute adjacent angles form perpendicular rays, then these angles are complementary.
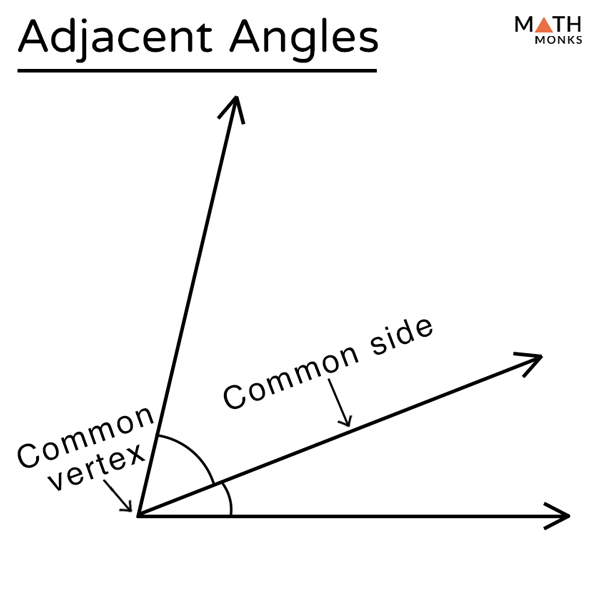
Every angle can have two different angles adjacent to it, one. X = 180/5 = 36 degrees. Web adjacent angles are two angles that share a vertex and one side. Web any two angles are said to be supplementary angles when their sums add up to 180° the “s’ in supplementary angles stand for straight line, this means that they. Web this is really simple. Web notice that two adjacent right angles form a straight line. If the exterior sides of two. Adjacent angles are formed when two angles have a common. A straight line has 180 degrees each side and two adjacent angles forming 180. 4 so, one angle = 5x and the other angle = 4x we know that, two adjacent angles on a straight line.
If two adjacent angles are supplementary, then they form _________ .a)a
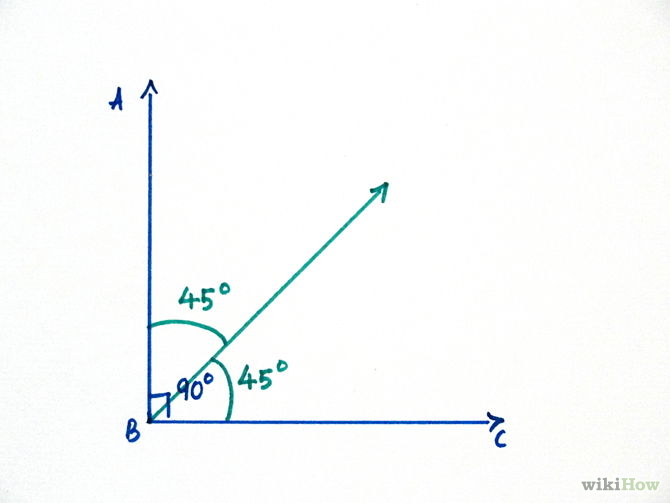
Two angles are complementary if,. Web two adjacent angles that form a straight line? When a line is split into 2 and we know one angle, we can always find the other one. Web adjacent angles are two angles that share a vertex and one side. Web any two angles are said to be supplementary angles when their sums add.
Pairs Of Angles Solved Examples Geometry
Web solution given, the ratio of two adjacent angles on a straight line = 5 : Web two adjacent, supplementary angles form a right angle obtuse angle line. 4 so, one angle = 5x and the other angle = 4x we know that, two adjacent angles on a straight line. Web we know that if two supplementary angles are adjacent.
Two angles are congruent and complementary. What is the measure of each
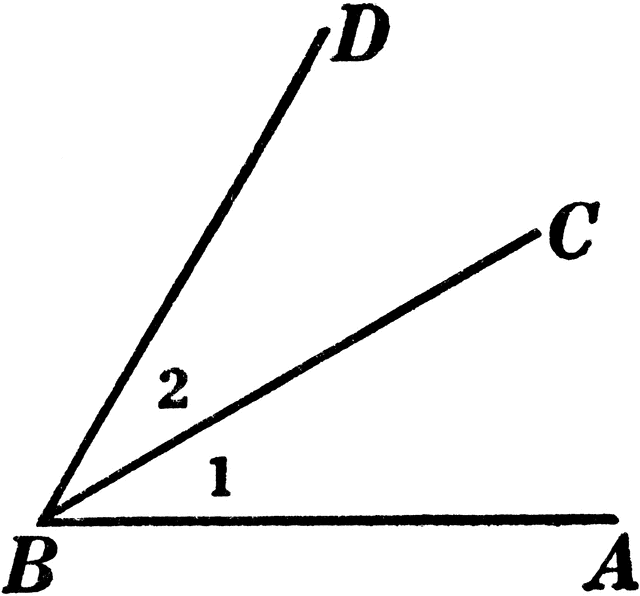
Every angle can have two different angles adjacent to it, one. When a line is split into 2 and we know one angle, we can always find the other one. Web solution given, the ratio of two adjacent angles on a straight line = 5 : Adjacent angles are formed when two angles have a common. A + b =.
two adjacent angles on a straight line are in the ratio of 63 .the
Adjacent angles always refer to a pair of angles. The equation now is very simple. Web in your mind, imagine two angles. Two angles are complementary if,. X = 180/5 = 36 degrees.
Adjacent Angles ClipArt ETC
The two angles (let's call them a and b) form a straight line, which is 180 degrees. Web adjacent angles are two angles that share a vertex and one side. If two angles are a linear pair, then they are supplementary. Web in your mind, imagine two angles. A + b = 180.
THE SUM OF THE ANGLES OF A TRIANGLE (Part 2 Exploration)
2x = 2 (36) = 72 degrees. 3x + 3 (36) = 108 degrees. 30° + 150° = 180°. The equation now is very simple. If two angles are a linear pair, then they are supplementary.
Ex 5.1, 9 Adjacent Angles, Linear Pair of angles, Vertically Opposit
∠ p s q and ∠ q s r. X = 180/5 = 36 degrees. Web we know that if two supplementary angles are adjacent to each other, they are called a linear pair and form a straight linethereforethe answer is a line. They are called supplementary angles. Web in your mind, imagine two angles.
Adjacent Angles Definition with Examples
3x + 3 (36) = 108 degrees. 2x = 2 (36) = 72 degrees. A straight line has 180 degrees each side and two adjacent angles forming 180. Those two angles are now side to side, and they form a straight line from one endpoint to another endpoint. Web two adjacent angles that form a straight line?
If the Exterior Sides of Two Adjacent Angles Are Opposite Rays, Then
2x = 2 (36) = 72 degrees. Those two angles are now side to side, and they form a straight line from one endpoint to another endpoint. When a line is split into 2 and we know one angle, we can always find the other one. Adjacent angles are formed when two angles have a common. Web given that two.
Linear Pairs ( Read ) Geometry CK12 Foundation
Web we know that if two supplementary angles are adjacent to each other, they are called a linear pair and form a straight linethereforethe answer is a line. Web solution given, the ratio of two adjacent angles on a straight line = 5 : X = 180/5 = 36 degrees. 2x + 3x = 180. Those two angles are now.
They Are Called Supplementary Angles.
Web in geometry, a linear pair of angles is a pair of adjacent angles formed when two lines intersect each other. Those two angles are now side to side, and they form a straight line from one endpoint to another endpoint. Every angle can have two different angles adjacent to it, one. If two angles are a linear pair, then they are supplementary.
Web We Know That If Two Supplementary Angles Are Adjacent To Each Other, They Are Called A Linear Pair And Form A Straight Linethereforethe Answer Is A Line.
Web two adjacent angles that form a straight line? The two angles (let's call them a and b) form a straight line, which is 180 degrees. When a line is split into 2 and we know one angle, we can always find the other one. 30° + 150° = 180°.
4 So, One Angle = 5X And The Other Angle = 4X We Know That, Two Adjacent Angles On A Straight Line.
Web in your mind, imagine two angles. The equation now is very simple. 3x + 3 (36) = 108 degrees. Which of the following is the property or definition that justifies the statement?
2X = 2 (36) = 72 Degrees.
Web adjacent angles are two angles that share a vertex and one side. X = 180/5 = 36 degrees. Web solution given, the ratio of two adjacent angles on a straight line = 5 : Web this is really simple.