Parametric Vector Form
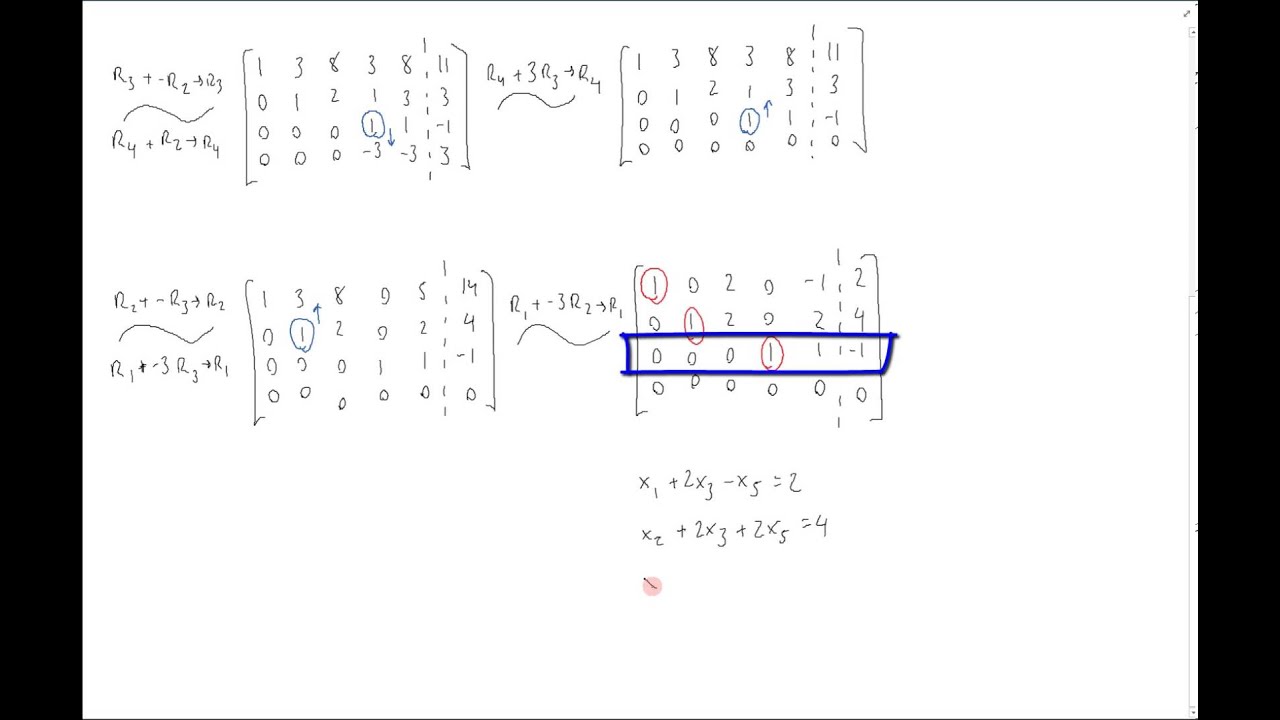
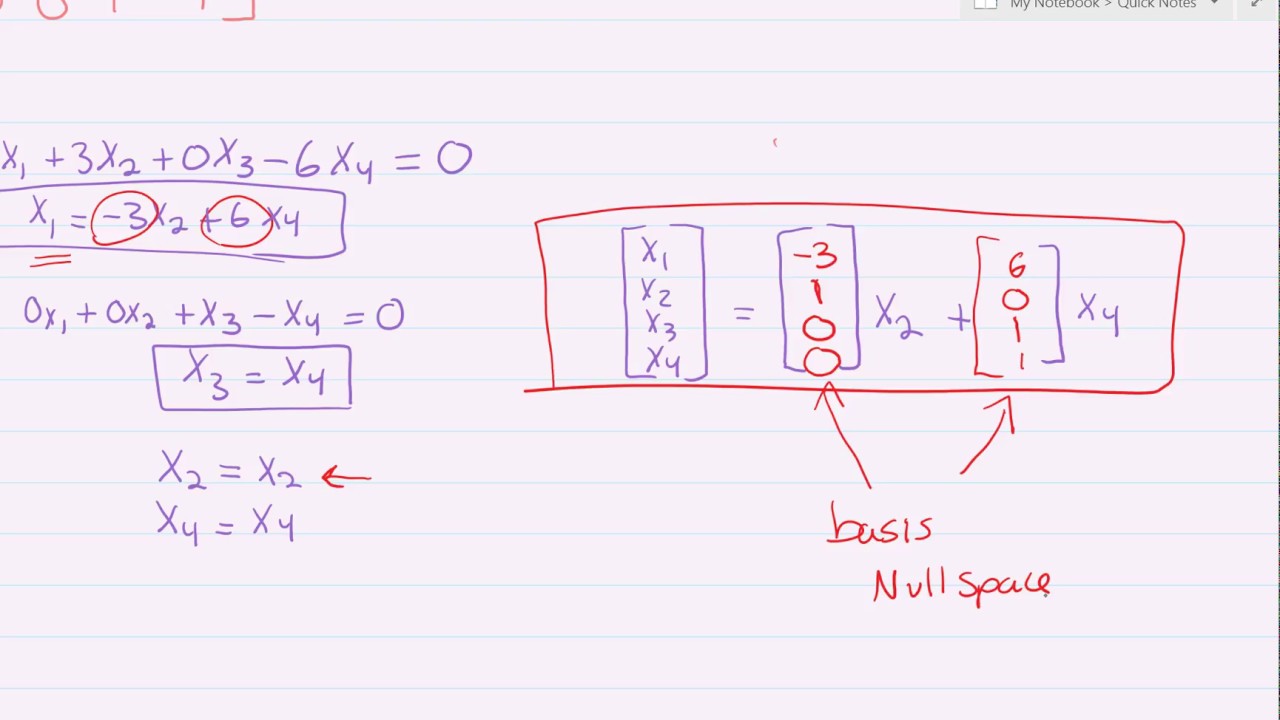
Parametric Vector Form - We emphasize the following fact in particular. This is also the process of finding the basis of the null space. X = ( x 1 x 2) = x 2 ( 3 1) + ( − 3 0). Multiplying a vector by a scalar. Web this is called a parametric equation or a parametric vector form of the solution. Web answering your question, you need a parametric vector solution set because the system of equations that is provided to you is underconstrained, that is, the number of variables is greater than the number of equations. Magnitude & direction to component. Wait a moment and try again. We turn the above system into a vector equation: (a) 1 2 2 4 # (b) 2 66 66 66 4 1 2 3 2 1 4 4 0 3 77 77 77 5 (c.
Note as well that while these forms can also be useful for lines in two dimensional space. We emphasize the following fact in particular. Web the one on the form $(x,y,z) = (x_0,y_0,z_0) + t (a,b,c)$. Web adding vectors algebraically & graphically. We turn the above system into a vector equation: And so, you must express the variables x1 and x2 in terms of x3 and x4 (free variables). 1 find a parametric vector form for the solution set of the equation ax~ =~0 for the following matrices a: Example it is sometimes useful to introduce new letters for the parameters. { x 1 = 3 x 2 − 3 x 2 = x 2 + 0. (0, −3, 0) − (6, 0, 0) = (−6, −3, 0) ( 0, − 3, 0) − ( 6, 0, 0) = ( − 6, − 3, 0) (0, 0, 2) − (6, 0, 0) =.
Where $(x_0,y_0,z_0)$ is the starting position (vector) and $(a,b,c)$ is a direction vector of the line. 1 find a parametric vector form for the solution set of the equation ax~ =~0 for the following matrices a: Sometimes the parametric equations for the individual scalar output variables are combined into a single parametric equation in vectors : Note as well that while these forms can also be useful for lines in two dimensional space. A point ( x, y) is on the unit circle if and only if there is a value of t such that these two equations generate that point. X1 = 1 + 2λ , x2 = 3 + 4λ , x3 = 5 + 6λ , x 1 = 1 + 2 λ , x 2 = 3 + 4 λ , x 3 = 5 + 6 λ , then the parametric vector form would be. And so, you must express the variables x1 and x2 in terms of x3 and x4 (free variables). Here is my working out: This called a parameterized equation for the same line. Web we can write the parametric form as follows:
Example Parametric Vector Form of Solution YouTube
Web answering your question, you need a parametric vector solution set because the system of equations that is provided to you is underconstrained, that is, the number of variables is greater than the number of equations. Web the one on the form $(x,y,z) = (x_0,y_0,z_0) + t (a,b,c)$. Web i know the vector form is x = p + td,.
4.2.3 Vector, Cartesian and Parametric Forms YouTube
{ x 1 = 3 x 2 − 3 x 2 = x 2 + 0. It is an expression that produces all points. Sometimes the parametric equations for the individual scalar output variables are combined into a single parametric equation in vectors : And so, you must express the variables x1 and x2 in terms of x3 and x4.
Solved Describe all solutions of Ax=0 in parametric vector
Web parametric forms in vector notation while you can certainly write parametric solutions in point notation, it turns out that vector notation is ideally suited to writing down parametric forms of solutions. Polar functions are graphed using polar coordinates, i.e., they take an angle as an input and output a radius! If you have a general solution for example. The.
Sec 1.5 Rec parametric vector form YouTube
(x, y, z) = (1 − 5z, − 1 − 2z, z) z any real number. Web this video shows an example of how to write the solution set of a system of linear equations in parametric vector form. This is also the process of finding the basis of the null space. Magnitude & direction to component. Web this video.
1.5 Parametric Vector FormSolving Ax=b in Parametric Vector Form
X1 = 1 + 2λ , x2 = 3 + 4λ , x3 = 5 + 6λ , x 1 = 1 + 2 λ , x 2 = 3 + 4 λ , x 3 = 5 + 6 λ , then the parametric vector form would be. Web adding vectors algebraically & graphically. 1 find a parametric vector.
Parametric Vector at Collection of Parametric Vector
Multiplying a vector by a scalar. This called a parameterized equation for the same line. The symmetric equations of a line are obtained by eliminating the parameter tfrom theparametric equations. But probably it means something like this: Can be written as follows:
Solved Find the parametric vector form of the solution of
Web parametric forms in vector notation while you can certainly write parametric solutions in point notation, it turns out that vector notation is ideally suited to writing down parametric forms of solutions. If you have a general solution for example. A common parametric vector form uses the free variables as the parameters s1 through s m. Web finding vector and.
Vector Parametric Form Flat Mathematics Stack Exchange
Span { ( 3 1) } + ( − 3 0). If you have a general solution for example. X = ( x 1 x 2) = x 2 ( 3 1) + ( − 3 0). Web parametric forms in vector notation while you can certainly write parametric solutions in point notation, it turns out that vector notation is.
202.3d Parametric Vector Form YouTube
Web what is a parametric vector form? { x 1 = 3 x 2 − 3 x 2 = x 2 + 0. (x, y, z) = (1 − 5z, − 1 − 2z, z) z any real number. Move all free variables to the right hand side of the equations. Web the one on the form $(x,y,z) = (x_0,y_0,z_0).
Parametric Vector Form and Free Variables [Passing Linear Algebra
X = ( x 1 x 2) = x 2 ( 3 1) + ( − 3 0). Web the parametric form {x = 1 − 5z y = − 1 − 2z. We turn the above system into a vector equation: Web what is a parametric vector form? Wait a moment and try again.
Wait A Moment And Try Again.
This is also the process of finding the basis of the null space. (a) 1 2 2 4 # (b) 2 66 66 66 4 1 2 3 2 1 4 4 0 3 77 77 77 5 (c. The set of solutions to a homogeneous equation ax = 0 is a span. Web this is called the parametric vector form of the solution.
Write The Corresponding (Solved) System Of Linear Equations.
Terminology is not altogether standard so check with your instructors. This called a parameterized equation for the same line. Matrix, the one with numbers, arranged with rows and columns, is extremely useful in most scientific fields. In this case, the solution set can be written as span {v 3, v 6, v 8}.
(X, Y, Z) = (1 − 5Z, − 1 − 2Z, Z) Z Any Real Number.
Where $(x_0,y_0,z_0)$ is the starting position (vector) and $(a,b,c)$ is a direction vector of the line. Web the parametric form {x = 1 − 5z y = − 1 − 2z. If you have a general solution for example. So my vectors are going to be these two points minus the original one i found.
Web What Is A Parametric Vector Form?
A common parametric vector form uses the free variables as the parameters s1 through s m. Sometimes the parametric equations for the individual scalar output variables are combined into a single parametric equation in vectors : Learn about these functions and how we apply the concepts of the derivative and the integral on them. Magnitude & direction to component.