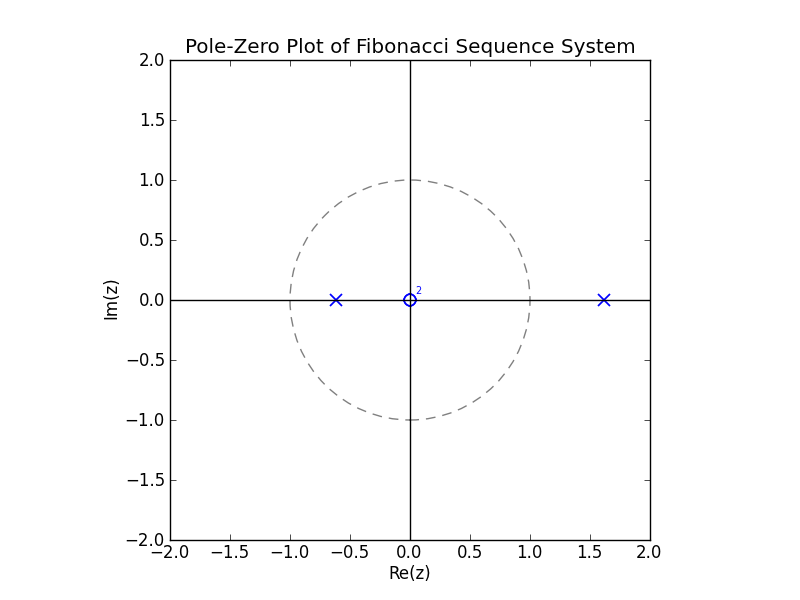
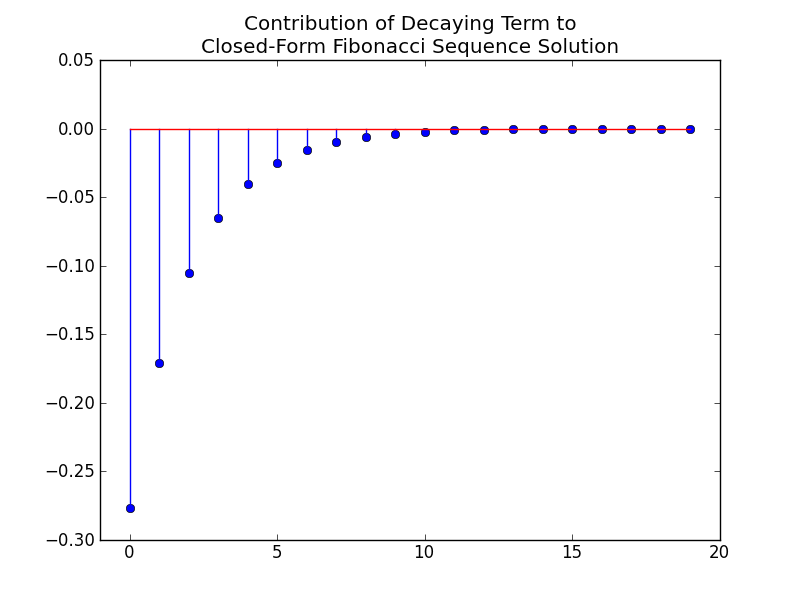
Closed Form Fibonacci Sequence
Closed Form Fibonacci Sequence - Consider a sum of the form nx−1 j=0 (f(a1n+ b1j + c1)f(a2n+ b2j + c2).f(akn+ bkj +ck)). F0 = 0 f1 = 1 fi = fi 1 +fi 2; Web justin uses the method of characteristic roots to find the closed form solution to the fibonacci sequence. Web proof of fibonacci sequence closed form k. The fibonacci sequence is the sequence (f n)n∈n0 ( f n) n ∈ n 0 satisfying f 0 = 0 f 0 = 0, f 1 = 1 f 1 = 1, and In either case fibonacci is the sum of the two previous terms. The fibonacci word is formed by repeated concatenation in the same way that the fibonacci numbers are formed by repeated addition. As a result of the definition ( 1 ), it is conventional to define. Fibonacci numbers can be viewed as a particular case of the fibonacci polynomials with. In particular, the shape of many naturally occurring biological organisms is governed by the fibonacci sequence and its close relative, the golden ratio.
The sequence appears in many settings in mathematics and in other sciences. I have this recursive fibonacci function: Since the fibonacci sequence is defined as fn =fn−1 +fn−2, we solve the equation x2 − x − 1 = 0 to find that r1 = 1+ 5√ 2 and r2 = 1− 5√ 2. And q = 1 p 5 2: Answered dec 12, 2011 at 15:56. Web a closed form of the fibonacci sequence. So fib (10) = fib (9) + fib (8). Are 1, 1, 2, 3, 5, 8, 13, 21,. The question also shows up in competitive programming where really large fibonacci numbers are required. X n = ∑ k = 0 n − 1 2 x 2 k if n is odd, and
Or 0 1 1 2 3 5. And q = 1 p 5 2: Web justin uses the method of characteristic roots to find the closed form solution to the fibonacci sequence. Since the fibonacci sequence is defined as fn =fn−1 +fn−2, we solve the equation x2 − x − 1 = 0 to find that r1 = 1+ 5√ 2 and r2 = 1− 5√ 2. For large , the computation of both of these values can be equally as tedious. Web closed form fibonacci. I don’t see any way to derive this directly from the corresponding closed form for the fibonacci numbers, however. Web if you set f ( 0) = 0 and f ( 1) = 1, as with the fibonacci numbers, the closed form is. I'm trying to find the closed form of the fibonacci recurrence but, out of curiosity, in a particular way with limited starting information. The trick is in doing the power function.
(PDF) Factored closedform expressions for the sums of cubes of
We prove that such a sum always has a closed form in the sense that it evaluates to Web if you set f ( 0) = 0 and f ( 1) = 1, as with the fibonacci numbers, the closed form is. Web closed form of the fibonacci sequence: You’d expect the closed form solution with all its beauty to.
Fibonacci Sequence Poetry? Yes, Please! Tom Liam Lynch, Ed.D.
Web the fibonacci numbers are the sequence of numbers defined by the linear recurrence equation (1) with. Web with some math, one can also get a closed form expression (that involves the golden ratio, ϕ). The fibonacci sequence is the sequence (f n)n∈n0 ( f n) n ∈ n 0 satisfying f 0 = 0 f 0 = 0, f.
PPT Generalized Fibonacci Sequence a n = Aa n1 + Ba n2 By
We know that f0 =f1 = 1. Web suppose {f(n)} is a sequence that satisfies a recurrence with constant coefficients whose associated polynomial equation has distinct roots. So fib (10) = fib (9) + fib (8). I am aware that the fibonacci recurrence can be solved fairly easily using the characteristic root technique (and its corresponding linear algebra interpretation): I.
The Fibonacci Numbers Determining a Closed Form YouTube
Solving using the characteristic root method. In either case fibonacci is the sum of the two previous terms. Web closed form fibonacci. Web justin uses the method of characteristic roots to find the closed form solution to the fibonacci sequence. Subramani lcsee, west virginia university, morgantown, wv fksmani@csee.wvu.edug 1 fibonacci sequence the fibonacci sequence is dened as follows:
Example Closed Form of the Fibonacci Sequence YouTube
Answered dec 12, 2011 at 15:56. Web suppose {f(n)} is a sequence that satisfies a recurrence with constant coefficients whose associated polynomial equation has distinct roots. Web there is a closed form for the fibonacci sequence that can be obtained via generating functions. Web proof of fibonacci sequence closed form k. (1) the formula above is recursive relation and in.
vsergeev's dev site closedform solution for the fibonacci sequence
The fibonacci sequence is the sequence (f n)n∈n0 ( f n) n ∈ n 0 satisfying f 0 = 0 f 0 = 0, f 1 = 1 f 1 = 1, and Web with some math, one can also get a closed form expression (that involves the golden ratio, ϕ). But there should be a more concrete proof for.
vsergeev's dev site closedform solution for the fibonacci sequence
After some calculations the only thing i get is: Web the fibonacci numbers are the sequence of numbers defined by the linear recurrence equation (1) with. In either case fibonacci is the sum of the two previous terms. The closed formula for fibonacci numbers we shall give a derivation of the closed formula for the fibonacci sequence fn here. Web.
Solved Derive the closed form of the Fibonacci sequence.
Web closed form of the fibonacci sequence back to home page (25 feb 2021) this is a pretty standard exercise in linear algebra to get a feeling for how to use eigenvalues and eigenvectors. The closed formula for fibonacci numbers we shall give a derivation of the closed formula for the fibonacci sequence fn here. The sequence appears in many.
Solved Derive the closed form of the Fibonacci sequence. The
I am aware that the fibonacci recurrence can be solved fairly easily using the characteristic root technique (and its corresponding linear algebra interpretation): It has become known as binet's formula, named after french mathematician jacques philippe marie binet, though it was already known by abraham de moivre and daniel bernoulli: Web closed form of the fibonacci sequence back to home.
Sequences closedform formula vs recursively defined YouTube
I am aware that the fibonacci recurrence can be solved fairly easily using the characteristic root technique (and its corresponding linear algebra interpretation): Or 0 1 1 2 3 5. Consider a sum of the form nx−1 j=0 (f(a1n+ b1j + c1)f(a2n+ b2j + c2).f(akn+ bkj +ck)). Look for solutions of the form f ( n) = r n, then.
X N = ∑ K = 0 N − 1 2 X 2 K If N Is Odd, And
This is defined as either 1 1 2 3 5. A favorite programming test question is the fibonacci sequence. Web proof of fibonacci sequence closed form k. The closed formula for fibonacci numbers we shall give a derivation of the closed formula for the fibonacci sequence fn here.
(1) The Formula Above Is Recursive Relation And In Order To Compute We Must Be Able To Computer And.
By doing this matrix ^ n (in a clever way) you can compute fib (n) in o (lg n). In either case fibonacci is the sum of the two previous terms. As a result of the definition ( 1 ), it is conventional to define. The trick is in doing the power function.
For Large , The Computation Of Both Of These Values Can Be Equally As Tedious.
Web there is a closed form for the fibonacci sequence that can be obtained via generating functions. Web justin uses the method of characteristic roots to find the closed form solution to the fibonacci sequence. Remarks one could get (1) by the general method of solving recurrences: F0 = 0 f1 = 1 fi = fi 1 +fi 2;
F ( N) = ( 1 + 3) N − ( 1 − 3) N 2 3;
We looked at the fibonacci sequence defined recursively by , , and for : I don’t see any way to derive this directly from the corresponding closed form for the fibonacci numbers, however. It has become known as binet's formula, named after french mathematician jacques philippe marie binet, though it was already known by abraham de moivre and daniel bernoulli: Consider a sum of the form nx−1 j=0 (f(a1n+ b1j + c1)f(a2n+ b2j + c2).f(akn+ bkj +ck)).