A+Bi Standard Form
A+Bi Standard Form - A + bi c − di. Web 1 review of complex numbers complex numbers can be written as z = a + bi, where a and b are real numbers, and i = 1. A is a number whose absolute value is a decimal number greater than or equal to 1, and less than 10: Web thus we can convert any complex number in the standard (cartesian) form z = a + bi into its polar form. Learn to write complex numbers in the (a+bi) form. This form, a + bi, is called the standard form of a. = (a + bi)(c + di) (c − di)(c + di). View full question and answer details:. Web algebra algebra questions and answers write the expression in the standard form a+bi. Web a complex number is expressed in standard form when written \(a+bi\) where \(a\) is the real part and \(bi\) is the imaginary part.
Web algebra algebra questions and answers write the expression in the standard form a+bi. Web to multiply two complex numbers z1 = a + bi and z2 = c + di, use the formula: Discover how to write complex numbers in standard form after basic. Pay attention to the second term −i and the exponents on that term. 147 views 1 year ago. Complex numbers have the form a+bi a + b i, where a and b are real numbers and i is the square root of −1 − 1. Learn to write complex numbers in the (a+bi) form. Web write the sum or difference in the standard form a + bi. Web simplify factor expand gcf lcm enter expression, e.g. A × 10b a × 10 b.
Web write the sum or difference in the standard form a + bi. Web thus we can convert any complex number in the standard (cartesian) form z = a + bi into its polar form. All real numbers can be written as complex numbers by. When using complex numbers, it is important to write our answer in this form. A is a number whose absolute value is a decimal number greater than or equal to 1, and less than 10: Web standard form format is: Complex numbers have the form a+bi a + b i, where a and b are real numbers and i is the square root of −1 − 1. For example, \(5+2i\) is a. Type your answer in the form a + bi.) this problem. A complex number is a number that can be.
How do you write (2i) / (42i) in the "a+bi" form? Socratic
All real numbers can be written as complex numbers by setting b = 0. Web see examples of imaginary numbers. Web this video shows the default or standard form of a complex number. Web to multiply two complex numbers z1 = a + bi and z2 = c + di, use the formula: Learn to write complex numbers in the.
Multiply. Write the answer in a+bi form YouTube
Web 1 review of complex numbers complex numbers can be written as z = a + bi, where a and b are real numbers, and i = 1. Complex numbers have the form a+bi a + b i, where a and b are real numbers and i is the square root of −1 − 1. Learn to write complex numbers.
Add, Subtract, Multiply Complex Numbers of the form a + bi YouTube
Web algebra algebra questions and answers write the expression in the standard form a+bi. My math professor suggested i use your algebrator product to help. Web simplify factor expand gcf lcm enter expression, e.g. Web standard form format is: This form, a + bi, is called the standard form of a.
write in a+bi form 2 YouTube
Pay attention to the second term −i and the exponents on that term. Web write the sum or difference in the standard form a + bi. All real numbers can be written as complex numbers by. A is a number whose absolute value is a decimal number greater than or equal to 1, and less than 10: For example, \(5+2i\).
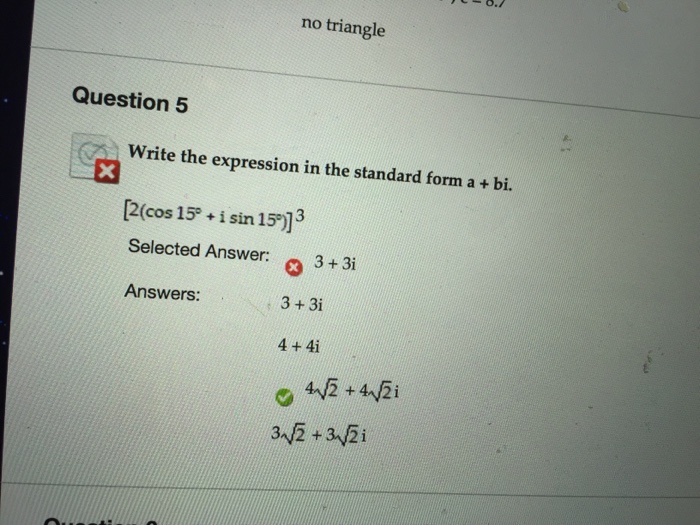
Solved Write the expression in the standard form a + bi. (1
Web to multiply two complex numbers z1 = a + bi and z2 = c + di, use the formula: All real numbers can be written as complex numbers by. Web simplify factor expand gcf lcm enter expression, e.g. Web see examples of imaginary numbers. Type your answer in the form a + bi.) this problem.
SOLVEDSimplify. Write each result in a + bi form. (8\sqrt{5})(2
A complex number is a number that can be. Web this video shows the default or standard form of a complex number. Web expressing a complex fraction in the standard form a + bi. Web 1 review of complex numbers complex numbers can be written as z = a + bi, where a and b are real numbers, and i.
Solved Write the expression in the standard form a + bi. [2
Multiply both numerator and denominator by the complex conjugate of the denominator, then simplify: Since any exponent on the first term of 1 is simply 1, we can ignore that term. Web thus we can convert any complex number in the standard (cartesian) form z = a + bi into its polar form. A × 10b a × 10 b..
13 Writing Complex Numbers in a + bi Form (1.3) YouTube
Type your answer in the form a + bi.) this problem. Web to multiply two complex numbers z1 = a + bi and z2 = c + di, use the formula: 5+i1−i 5+i1−i= (simplify your answer. = (a + bi)(c + di) (c − di)(c + di). Learn to write complex numbers in the (a+bi) form.
Write Complex Numbers in the Form a+bi YouTube
A complex number is a number that can be. Since any exponent on the first term of 1 is simply 1, we can ignore that term. All real numbers can be written as complex numbers by setting b = 0. Web expressing a complex fraction in the standard form a + bi. Complex numbers have the form a+bi a +.
Solved Write the expression in the standard form a + bi. If
A + bi c − di. My math professor suggested i use your algebrator product to help. 5+i1−i 5+i1−i= (simplify your answer. Web see examples of imaginary numbers. Type your answer in the form a + bi.) this problem.
Discover How To Write Complex Numbers In Standard Form After Basic.
= (a + bi)(c + di) (c − di)(c + di). Web simplify factor expand gcf lcm enter expression, e.g. Web to multiply two complex numbers z1 = a + bi and z2 = c + di, use the formula: This form, a + bi, is called the standard form of a.
Web A Complex Number Is Expressed In Standard Form When Written \(A+Bi\) Where \(A\) Is The Real Part And \(Bi\) Is The Imaginary Part.
Web expressing a complex fraction in the standard form a + bi. What is a complex number? Complex numbers have the form a+bi a + b i, where a and b are real numbers and i is the square root of −1 − 1. Web this video shows the default or standard form of a complex number.
Since Any Exponent On The First Term Of 1 Is Simply 1, We Can Ignore That Term.
Multiply both numerator and denominator by the complex conjugate of the denominator, then simplify: My math professor suggested i use your algebrator product to help. Web complex numbers have the form a + bi, where a and b are real numbers and i is the square root of −1. When using complex numbers, it is important to write our answer in this form.
Web Standard Form Format Is:
A + bi c − di. A complex number is a number that can be. Web the standard form of a complex number is a +bi a + b i where a a and b b are real numbers and they can be anything, positive, negative, zero, integers, fractions,. Learn to write complex numbers in the (a+bi) form.